标准偏差公式,标准偏差计算步骤



2022-05-07 14:07:08

2022-02-18 09:16:01

2021-11-23 16:30:32

2021-11-23 15:34:03

2021-11-10 15:06:42
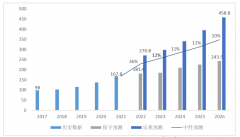
近几年来,太阳能光伏和储能市场异常火爆。据欧洲光伏产业协会发布的《全球市场展望太阳...

大理石瓷砖,是指具有天然大理石逼真纹理、色彩和质感的一类瓷砖产品,其具有天然大理石...

电子灌封胶有不同种类,目前使用最为广泛的有导热灌封胶、有机硅灌封胶、环氧树脂胶灌封...

如石、如玉、如钻的本色出演,筑就一个又一个建筑的舞台,出色的演绎空间美学。 玉胜天然...

万千年的淘洗,成就无暇的美玉,1600度的余温,筑就了颜如玉的科素花岗玉。 捕捉凝练时,自...

SLD单组份有机硅产品通过接触大气湿,气固化。固化过程开始于外表面并向内进行、不建议超...

抛光砖: 抛光砖是通体砖坯体的表面经过打磨而成的一种光亮的砖,属通体砖的一种。相对通...

在半导体封测的整个工艺流程中,作为材料部分的工业粘合剂,即工业胶水,一般都是作为辅...

图书馆不在于高端、大气,但必有浩瀚,也许,人处于其间不过渺小若埃,也许,空间环境不...

近年来,随着汽车产业加速向新能源智能汽车发展,全球范围内的新能源汽车销量开始持续高...
